- Vous n'êtes pas identifié.
Annonce
#1 2017-05-05 02:10:14 fonction de courbe avec curseur
- AcousticQuantum
- membre
- Date d'inscription: 2014-11-25
- Messages: 33
fonction de courbe avec curseur
Bonjour,
Je souhaiterais réaliser quelque chose qu'il semble facile à faire, étant donné qu'il s'agit d'une petite application que l'on retrouve partout - même dans paint ! ![]()
En effet, même dans ce puissant logiciel ultra développé fourni gracieusement avec windows, l'outil "courbe" fonctionne de la manière suivante: on sélectionne le mode courbe, on trace un trait droit, puis on clique n'importe ou sur ce trait dessiné, et le point sélectionné se déplace avec la souris, formant une magnifique courbe dont le tracé se fait tout seul par le programme... C'est à peu de chose près ce que je souhaite reproduire...
Cela dit, je bloque pourtant sur un problème mathématique que mon faible niveau ne parvient pas à dépasser...
Parce qu'un dessin vaut mieux qu'un long discours, voici ci-joint un croquis qui me permettra d'illustrer mon propos...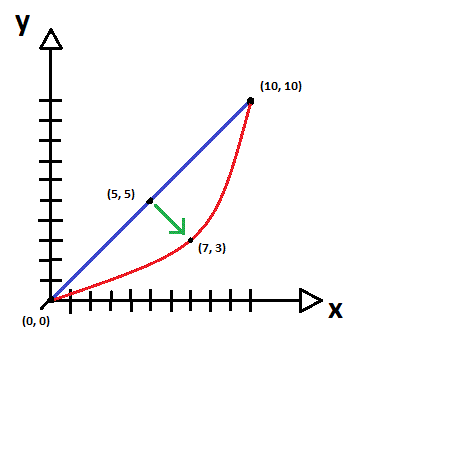
Sur ce graphique, on peut voir un premier segment, en bleu, qui peut être décrit par une fonction du 1er degré tout ce qu'il y a de plus simple, de type y = x.
Ce que j'aimerais parvenir à faire, c'est, à partir d'une poignée, ici à la moitié du 1er segment, en (5,5) donc, pouvoir modifier mon segment et le rendre courbe. Ainsi, ma courbe rouge est délimitée par les mêmes extrémités que mon segment bleu et je peux décrire la courbe que je souhaite à travers cette seule poignée...
Plus que le rendu visuel, ce que je souhaite en fait, c'est pouvoir définir la fonction résultante, cette fonction dont la représentation graphique correspond justement à cette courbe créée. Cela afin de permettre, plus tard, de faire varier des valeurs en fonction d'elle, selon la courbe que j'aurais dessinée.
Voilà, j'espère que mon explication est claire et que quelqu'un pourra m'aider, j'ai les neurones en surchauffe! ![]()
EDIT:
J'ai trouvé un moyen afin de convertir en fonction du second degré, mais le résultat obtenu n'est pas celui désiré... Selon où l'on place la poignée, des creux ou des bosses peuvent se former, alors que je souhaite simplement créer une courbe tout ce qu'il y a de plus simple et de plus lisse, reliant mes points 3 points (point de départ, d'arrivée et poignée)... J'en conclu donc que la fonction que je dois créer n'est pas de type du second degré...
Voici mon code test pour le second degré:
PVector poignee;
boolean poigneeSelected = false;
float w, h;
float px, py;
int cadre = 100;
void setup(){
size(400, 400);
stroke(255);
noFill();
rectMode(CENTER);
w = width - (cadre * 2);
h = height - (cadre * 2);
poignee = new PVector(w/2, h/2);
}
void draw(){
background(0);
translate(cadre, cadre);
px = poignee.x;
py = h - poignee.y;
for(int x = 0; x < w; x++){
// conversion en fonction du second degré
float a = ( (h/w) - (py / px) ) / (w - px);
float b = (py / px) - a * px;
float y = (a * x*x) + (b * x);
//y = constrain(y, 0, h); // on restreind les valeurs aux limites
point(x, h - y); // points de la courbe
}
rect(poignee.x, poignee.y, 10, 10); // poignee
}
void mousePressed(){
if(mouseX > poignee.x + cadre - 5 && mouseX < poignee.x + cadre + 5 &&
mouseY > poignee.y + cadre - 5 && mouseY < poignee.y + cadre + 5){
poigneeSelected = true;
}
else{
poigneeSelected = false;
}
}
void mouseDragged(){
if (poigneeSelected){
poignee.x = mouseX - cadre;
poignee.y = mouseY - cadre;
}
}
Hors ligne
#2 2017-05-05 10:07:06 Re : fonction de courbe avec curseur
Re: fonction de courbe avec curseur
Hello,
Un mot clef qui te manque pour tes recherches est "Courbe de Bézier".
Par contre, tu n'obtiendras pas d'équation de la forme y=f(x) car les courbes de Bézier ne s'appuient pas sur un repère.
Bon courage.
L'Amour au Peuple !
Hors ligne
#3 2017-05-08 00:33:01 Re : fonction de courbe avec curseur
- Mushussu
- membre
- Lieu: Orléans
- Date d'inscription: 2012-05-24
- Messages: 802
Re: fonction de courbe avec curseur
Bonsoir,
Une courbe qui passe par trois points est une parabole, donc elle est de la forme
y = ax2 + bx + c
tu te retrouve avec un système de trois équation une pour chaque point a trois inconnus a, b, c.
Donc tu peux facilement trouver l'équation qui passe par les trois points.
J'ai fait cela dans le train, ce n'est pas exactement ce que tu souhaites, mais peut te donner des pistes.
PVector positionSouris;
PVector debut = new PVector(100, 100);
PVector fin = new PVector(700, 500);
float definition;
void setup() {
size(800, 600);
noFill();
positionSouris = new PVector(0, 0);
definition = 100;
}
void draw() {
background(255);
if (mousePressed) {
PVector pointPrecedent = debut.copy();
for (float t = 1 / definition; t < 1; t = t + 1 / definition) {
PVector point = new PVector((1 - t * t) * debut.x + 2 * t * (1 - t) * mouseX + t * t * fin.x, (1 - t * t) * debut.y + 2 * t * (1 - t) * mouseY + t * t * fin.y);
line(pointPrecedent.x , pointPrecedent.y, point.x, point.y);
pointPrecedent.set(point);
}
} else {
line(debut.x, debut.y, fin.x, fin.y);
}
}Hors ligne
#4 2017-05-08 15:04:00 Re : fonction de courbe avec curseur
- AcousticQuantum
- membre
- Date d'inscription: 2014-11-25
- Messages: 33
Re: fonction de courbe avec curseur
Bonjour,
Merci à tous les 2 pour l'attention portée à mon message ![]()
Olivier,
Olivier a écrit:
Un mot clef qui te manque pour tes recherches est "Courbe de Bézier".
J'étais effectivement tombé sur les courbes de Béziers lors de mes recherches, mais comme tu l'indiques toi-même
Olivier a écrit:
tu n'obtiendras pas d'équation de la forme y=f(x)
hors, comme je l'avais expliqué dans mon premier message:
AcousticQuantum a écrit:
Plus que le rendu visuel, ce que je souhaite en fait, c'est pouvoir définir la fonction résultante, cette fonction dont la représentation graphique correspond justement à cette courbe créée. Cela afin de permettre, plus tard, de faire varier des valeurs en fonction d'elle, selon la courbe que j'aurais dessinée.
Mushussu,
Ton code m'a bluffé ![]() Cela ressemble très fort à ce que je souhaite faire en effet... et d'une simplicité (le nombre de ligne de code!)
Cela ressemble très fort à ce que je souhaite faire en effet... et d'une simplicité (le nombre de ligne de code!)
Mais je ne comprends pas la logique de la ligne principale:
PVector point = new PVector((1 - t * t) * debut.x + 2 * t * (1 - t) * mouseX + t * t * fin.x, (1 - t * t) * debut.y + 2 * t * (1 - t) * mouseY + t * t * fin.y);
Pourrais-tu m'expliquer la logique des valeurs placées dans le vecteur stp?
En ce qui concerne
Mushussu a écrit:
Une courbe qui passe par trois points est une parabole, donc elle est de la forme
y = ax2 + bx + c
tu te retrouve avec un système de trois équation une pour chaque point a trois inconnus a, b, c.
Donc tu peux facilement trouver l'équation qui passe par les trois points.
Ca fait longtemps que je suis sorti de l'école et mes cours de math sont loin derrière moi ![]()
Prenons l'exemple de 3 points A(0, 0), B(7, 3) et C(10, 10)
selon l'équation y = ax2 + bx +c nous obtenons donc
pour A:
0 = a * 0 * 0 + b * 0 + c <=> c = 0
pour B:
3 = a * 7 * 7 + b * 7 + c = 49 a + 7 b + 0 <=> 0 = 49 a + 7 b - 3
pour C:
10 = a * 10 * 10 + b * 10 + c = 100 a +10 b <=> 0 = 100 a + 10 b - 10
et donc, en reliant B et C:
49 a + 7 b - 3 = 100 a + 10 b - 10
<=> 51 a + 3b - 7 = 0
et je suis bloqué ici... comment trouver mes valeurs a et b à partir d'ici???
Sinon hier soir, j'avais finalement trouvé une solution qui me convenait, mais beaucoup plus laborieuse que la tienne!!! En gros ma méthode: je connais la fonction de la tangente à mon curseur, et calcule simplement les tangentes de mes points d'extrémité. Je pars du point de mon curseur et me dirige vers mes points d'extrémité. A chaque itération, je bascule légèrement ma tangente afin qu'à l'arrivée elle corresponde avec les tangentes des extrémités. Ce basculement, cette variation de la tangente me donne une nouvelle fonction (du 1er degré) que je calcule. Et c'est à partir de cette fonction que je détermine les coordonnées de mon point...
Voici à quoi cela ressemble (c'est un peu brouillon, je travaillais à le rendre plus lisible et à l'épurer au moment où je suis venu vérifier mes messages sur ce site):
PVector A;
PVector B;
float w;
float cadre;
float x;
float y;
float xp;
float yp;
PVector poignee = new PVector();
float xAngle;
PVector xVec;
float a;
float b;
PVector f2;
void setup(){
size(600, 600);
background(0);
noFill();
ellipseMode(CENTER);
w = 400;
cadre = (height - w) / 2;
A = new PVector(0, 0); // point d'origine
B = new PVector(w, w); // point final
xp = w/2;
}
void draw(){
background(0);
translate(cadre, cadre);
if(xp < 0){
xp = 0;
}
if(xp > w){
xp = w;
}
// ligne curseur
x = 0;
while(x < w){
y = -x + w;
stroke(63);
point(x, w - y);
stroke(255);
x++;
}
// poignee
yp = -xp + w;
poignee.set(xp, yp);
ellipse(poignee.x, w - poignee.y, 3, 3);
float tgAngle = PI/4; // angle tangente
f2 = new PVector();
f2 = B.get();
f2.sub(poignee);
float f2Angle = PI/2 - f2.heading(); // angle vecteur MB
float angleDif = - tgAngle + f2Angle; // différence totale
xAngle = angleDif / xp;
x = xp;
int compt = 0;
while(x > 0){
xVec = PVector.fromAngle((compt+1) * xAngle); // difference d'angle au pas x
xVec.rotate(PI/4); // angle au pas x
a = xVec.y / xVec.x; // calcul de a
b = xVec.y - a * xVec.x; // calcul de b
y = a * compt + b; // fonction de la tengante au pas x
/*if(y > w - xp){ // constrain
y = w - xp;
}*/
point(x, y + xp);
x--;
compt++;
}
xAngle = angleDif / (w - xp); // différence pas à pas
x = xp;
compt = 0;
while(x < w){
xVec = PVector.fromAngle((compt+1) * xAngle); // difference d'angle au pas x
xVec.rotate(-PI/4); // angle au pas x
a = xVec.y / xVec.x; // calcul de a
b = xVec.y - a * xVec.x; // calcul de b
y = a * compt + b; // fonction de la tengante au pas x
/*if(y < -xp){ // constrain
y = -xp;
}*/
point(x, y + xp);
x++;
compt++;
}
}
void keyPressed(){
if (key == CODED){
if (keyCode == UP){
xp -= 10;
}
else if (keyCode == DOWN){
xp += 10;
}
}
}
void mouseDragged(){
xp = mouseY - cadre;
}
Hors ligne
#5 2017-05-08 21:10:35 Re : fonction de courbe avec curseur
- AcousticQuantum
- membre
- Date d'inscription: 2014-11-25
- Messages: 33
Re: fonction de courbe avec curseur
Re:
Pour l'équation du second trouvé, c'est bon j'ai trouvé... Par contre le résultat obtenu ne ressemble pas à ton programme et la courbe ner éagit pas comme je le souhaiterais...
Voici le résultat obtenu avec la solution y = ax2 + bx
int diamPoignee = 10;
int w = 300;
float cadre;
PVector ptA, ptB, ptC;
float a, b, y;
boolean poigneeSelected = false;
void setup(){
size(600, 600);
stroke(255);
noFill();
rectMode(CENTER);
cadre = (height - w) / 2;
ptA = new PVector(0, 0);
ptB = new PVector(w, w);
ptC = new PVector(w/2, w/2);
}
void draw(){
background(0);
translate(cadre, cadre);
a = (ptC.x - ptC.y) / ( ptC.x * (ptB.x - ptC.x) );
b = 1 - a * ptB.x;
for(int x = 0; x < w; x++){
y = a * x * x + b * x;
point(x, y);
}
rect(ptC.x, ptC.y, 10, 10); // poignee
}
void mousePressed(){
if(mouseX > ptC.x - diamPoignee/2 + cadre && mouseX < ptC.x + diamPoignee/2 + cadre &&
mouseY > ptC.y - diamPoignee/2 + cadre && mouseY < ptC.y + diamPoignee/2 + cadre){
poigneeSelected = true;
}
else{
poigneeSelected = false;
}
}
void mouseDragged(){
if (poigneeSelected){
ptC.x = mouseX - cadre;
ptC.y = mouseY - cadre;
}
}
Hors ligne
#6 2017-05-08 21:43:19 Re : fonction de courbe avec curseur
- Mushussu
- membre
- Lieu: Orléans
- Date d'inscription: 2012-05-24
- Messages: 802
Re: fonction de courbe avec curseur
Bonsoir,
pour A:
0 = a * 0 * 0 + b * 0 + c <=> c = 0
pour B:
3 = a * 7 * 7 + b * 7 + c = 49 a + 7 b + 0 <=> 0 = 49 a + 7 b - 3
pour C:
10 = a * 10 * 10 + b * 10 + c = 100 a +10 b <=> 0 = 100 a + 10 b - 10
10a = 1 - b
a = (1 - b) / 10
On remplace dans l'équation précédente :
0 = 49 * (1 - b) / 10 + 7b - 3
30 = 49(1 - b) + 70b
-19 = 21b
b = -19 / 21
et ainsi de suite.
Bon a priori, cela ne sert pas à grand chose, mais je continue mes recherches.
Le code amélioré :
PVector debut = new PVector(100, 100);
PVector fin = new PVector(700, 500);
void setup() {
size(800, 600);
noFill();
}
void draw() {
background(255);
if (mousePressed) {
bezier(debut.x, debut.y, mouseX, mouseY, mouseX, mouseY, fin.x, fin.y);
} else {
line(debut.x, debut.y, fin.x, fin.y);
}
}Hors ligne
#7 2017-05-09 04:23:59 Re : fonction de courbe avec curseur
- AcousticQuantum
- membre
- Date d'inscription: 2014-11-25
- Messages: 33
Re: fonction de courbe avec curseur
Bon, cela aura été un peu fastidieux, mais je suis parvenu à faire ce que je voulais ![]()
En gros, j'ai créé un petit objet que l'on peut placer où l'on souhaite sur notre canvas. Cet objet est un peu semblable à l'objet "map()" de processing, excepté que celui affiche un graphique que l'on peu manipuler et dont la courbe peut "étirer" la manière dont le nombre sera mappé...
Voici un petit exemple si quelqu'un souhaiterait voir le résultat ![]()
Curseur curseur;
void setup(){
println("move the cursor to see what happens");
println("or press the keys UP and DOWN");
size(400, 225);
colorMode(HSB);
curseur = new Curseur(150, 25, 100);
}
void draw(){
background(0);
curseur.show();
for(int i = 0; i < 255; i++){
float j = curseur.mapCurve(i, 0, 255);
fill(j, 255, 255);
noStroke();
rect(i+72, 150, 1, 50);
}
}
void keyPressed(){
if (key == CODED){
if (keyCode == UP){
curseur.xp -= 10;
}
else if (keyCode == DOWN){
curseur.xp += 10;
}
}
}
void mouseDragged(){
/*if(mouseX > curseur.xPos && mouseX < curseur.xPos + curseur.taille &&
mouseY > curseur.yPos && mouseY < curseur.yPos + curseur.taille){
curseur.xp = mouseY - curseur.yPos;
}*/
curseur.xp = mouseY - curseur.yPos;
}
class Curseur{
int xPos, yPos, taille;
float xp, yp, xAngle, angleDif, a, b;
PVector poignee = new PVector();
PVector f2, xVec;
boolean inverse;
Curseur(int _xPos, int _yPos, int _taille){
xPos = _xPos;
yPos = _yPos;
taille = _taille;
xp = taille/2;
}
void show(){
pushMatrix();
translate(xPos, yPos);
// bg
fill(7);
stroke(7);
rect(0, 0, taille, taille);
// limites curseur
if(xp < 0){ xp = 0; }
if(xp > taille){ xp = taille; }
// ligne curseur
stroke(63);
line(0, 0, taille, taille);
// curseur
yp = -xp + taille;
poignee.set(xp, yp);
stroke(255);
ellipse(poignee.x, taille - poignee.y, 3, 3);
float tgAngle = PI/4; // angle tangente
f2 = new PVector(taille, taille);
f2.sub(poignee);
float f2Angle = PI/2 - f2.heading(); // angle vecteur MB
angleDif = - tgAngle + f2Angle; // différence totale
inverse = true;
for(int x = 0; x < taille; x++){
float y = mapCurve(x, 0, taille);
point(x, y);
}
inverse = false;
popMatrix();
}
float mapCurve(int _abscisse, float min, float max){
float abscisse = float(_abscisse);
float ordonnee = 0;
float minPrim = map(min, min, max, 0, taille);
float maxPrim = map(max, min, max, 0, taille);
int abscissePrim = int(map(abscisse, min, max, 0, taille));
xAngle = angleDif / xp;
float x = xp;
int compt = 0;
while(x >= 0){
xVec = PVector.fromAngle((compt+1) * xAngle); // difference d'angle au pas x
xVec.rotate(PI/4); // angle au pas x
a = xVec.y / xVec.x; // calcul de a
b = xVec.y - a * xVec.x; // calcul de b
float y = a * compt + b; // fonction de la tengante au pas x
if(y > taille - xp){ y = taille - xp; } // constrain
if(x == abscissePrim){ ordonnee = y; }
x--;
compt++;
}
xAngle = angleDif / (taille - xp); // différence pas à pas
x = xp;
compt = 0;
while(x < taille){
xVec = PVector.fromAngle((compt+1) * xAngle); // difference d'angle au pas x
xVec.rotate(-PI/4); // angle au pas x
a = xVec.y / xVec.x; // calcul de a
b = xVec.y - a * xVec.x; // calcul de b
float y = a * compt + b; // fonction de la tengante au pas x
if(y < -xp){ y = -xp; } // constrain
if(x == abscissePrim){ ordonnee = y; }
x++;
compt++;
}
ordonnee += xp;
if(inverse){ordonnee = map(ordonnee, 0, taille, min, max);}
else{ordonnee = map(ordonnee, 0, taille, max, min);}
return ordonnee;
}
}
Maintenant que je l'ai fait, je me demande s'il n'y avait pas une librairie contenant un objet similaire lol
Si quelqu'un a une idée ou des commentaires sur ce code, il est le bienvenue! ![]()
A+ et merci encore à ceux qui ont passé du temps sur ce post! ![]()
Hors ligne
#8 2017-05-12 15:00:59 Re : fonction de courbe avec curseur
- jojolaglaise
- membre

- Lieu: Basse Normandie
- Date d'inscription: 2014-04-20
- Messages: 137
- Site web
Re: fonction de courbe avec curseur
joli tout ça !
Hors ligne
Pages: 1
- Accueil forums
- » Processing
- » fonction de courbe avec curseur
fil rss de cette discussion :
