- Vous n'êtes pas identifié.
Annonce
#1 2010-04-09 22:35:52 Diffusion-réaction 1D
- Staross
- membre
- Date d'inscription: 2008-04-03
- Messages: 322
Diffusion-réaction 1D
Un petit script qui résout des équations de diffusion-réaction en une dimension et fais un graphique temps/espace. Sans entrer dans les détails ces équations modélisent deux espèces chimiques qui diffusent (comme une goute d'encre dans de l'eau) et qui réagissent chimiquement. Ce genre d'équations sont utilisées en biologie par exemple, où on pense que la forme est générée par ce genre de mécanisme au cours du développement d'un organisme. Jetez un il la dessus par exemple :
http://books.google.com/books?id=X7Ju8F … mp;f=false
http://www.scholarpedia.org/article/Gie … ardt_model
Le code est très simple, y'a juste une boucle sur le temps et une boucle sur l'espace pour calculer la diffusion. En changeant les équations dans ces deux lignes (la partie entre le dt) et notamment les constantes on peut obtenir pas mal de comportement différents (vu la longueur du code c'est pas trop mal :).
A[i] = A[i] + dt*( 20*i/w*A[i]*A[i]*A[i]/(I[i]) + 0.5 -2*A[i] + 1*D2A[i] + 1*random(-1,1) ) ;
I[i] = I[i] + dt*( 1*A[i]*A[i]*A[i] -2*I[i] + 3*D2I[i] + 0*random(-1,1));
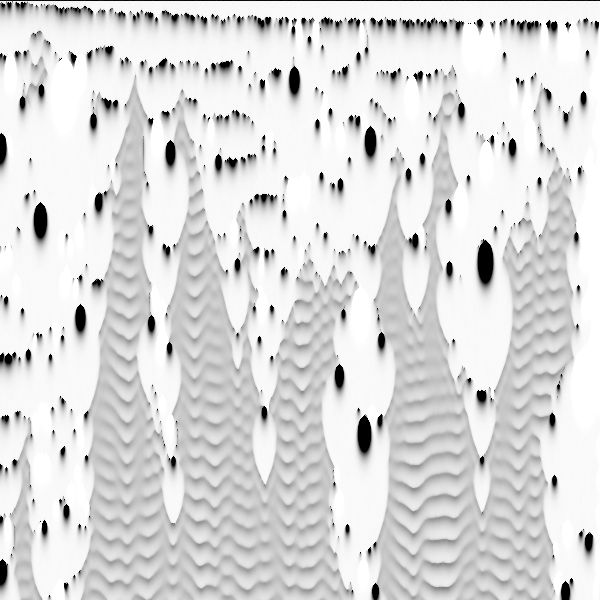

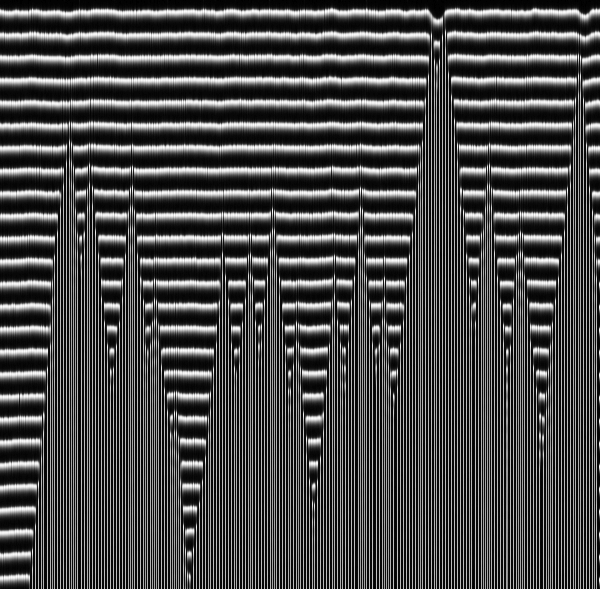



V'la le code :
import processing.opengl.*;
float pi = 3.1415;
int w = 600; //size of the window
int Nt = 600;
int strW = 2;
float A[] = new float[w];
float I[] = new float[w];
float C[] = new float[w];
float D2A[] = new float[w];
float D2I[] = new float[w];
float D2C[] = new float[w];
float dt = 0.05;
int t=0;
void setup(){
size(w,Nt);
smooth();
//noLoop();
//initial condition
for(int i=0;i<w; i++)
{
A[i] = random(0,1);
I[i] = random(0,1) + 20*i/w;
C[i] = random(0,1);
stroke(20*A[i]);
point(i,t);
}
t=t+1;
}
void draw(){
//fill(0);
if(t < Nt)
{
//background(255);
//Laplacian (for diffusion)
for(int i=1;i<w-1; i++)
{
D2A[i] = A[i-1] + A[i+1] - 2*A[i];
D2I[i] = I[i-1] + I[i+1] - 2*I[i];
D2C[i] = C[i-1] + C[i+1] - 2*C[i];
}
D2A[0] = A[1] - A[0];
D2I[0] = I[1] - I[0];
D2C[0] = C[1] - C[0];
for(int i=0;i<w; i++)
{
A[i] = A[i] + dt*( 20*i/w*A[i]*A[i]*A[i]/(I[i]) + 0.5 -2*A[i] + 1*D2A[i] + 1*random(-1,1) ) ;
I[i] = I[i] + dt*( 1*A[i]*A[i]*A[i] -2*I[i] + 3*D2I[i] + 0*random(-1,1));
//C[i] = C[i] + dt*( 1*A[i]*A[i]*A[i] -6*C[i] + 0.0 + 1*D2C[i]); //third chemical specie, not used here
//stroke(5*A[i],250-5*I[i],250-10*D2A[i]);
stroke(250-50*A[i]);
point(i,t);
}
t=t+1;
println(A[20]); //just to see if it doesn't explode
if(t == Nt) { saveFrame("out.tif"); }
}
}Dernière modification par Staross (2010-04-09 22:39:13)
Hors ligne
#2 2010-04-10 00:02:29 Re : Diffusion-réaction 1D
Re: Diffusion-réaction 1D
Super, merci! C'est peut-être même possible de faire du son avec ? Ça m'a rappelé ce programme sur openprocessing : http://openprocessing.org/visuals/?visualID=1263 Le modèle, inspiré de modélisation chimique à base d'automates cellulaires et les équations sont différents, mais visuellement y a kekchose
Hors ligne
#3 2010-04-12 23:04:31 Re : Diffusion-réaction 1D
- Staross
- membre
- Date d'inscription: 2008-04-03
- Messages: 322
Re: Diffusion-réaction 1D
C'est le même genre d'équations ouais. Pour faire du son on peut prendre ligne par ligne et lire ça comme si c'était de l'audio, mais pour faire 41000 échantillons par seconde en temps réel ça va être un peu chaud... j'avais essayé de faire ça rapidement en matlab avec la équation de ginzburg-landau, c'était pas inintéressant mais j'ai pas creusé beaucoup plus...
Hors ligne
