- Vous n'êtes pas identifié.
Annonce
#1 2006-05-13 12:14:28 Suite De Fibonacci et nombre d'or en Musique
- tobald
- modérateur
- Date d'inscription: 2008-03-28
- Messages: 499
Suite De Fibonacci et nombre d'or en Musique
Quel lien peut on trouver entre la suite de Fibonacci : 1 ;5 ; 8 ; 13 ;21 ... et certaines compositions musicales? L' exemple proposé ici est construit comme l'exposition d'une fugue. Le sujet à la première ligne est repris dans les lignes suivantes avec un certain décalage.Ce sujet est repris avec des imitations de plus en plus simples de ce qui vient d'être joué juste avant. La dernière ligne reprend une dernière fois le sujet à la fin ,pendant que la première ligne meurt petit à petit. Les différentes phrases musicales sont des nombres de la suite de Fibonacci ce qui donne un rythme vivant. Ce genre composition , avec un entrelacement de phrases musicales dont les longueurs en pulsations sont des nombres de la suite de Fibonacci, est utilisé de manière plus complexe dans la musique indonésienne.
source : http://expo.ifrance.com/lenombre/musique.htm
Le nombre d’or en Musique
1) – Intervalles musicaux et gammes.
On mesure l’intervalle séparant 2 notes de musique en calculant le rapport des fréquences caractérisant respectivement la note la plus aiguë et la note la plus grave.
La fréquence étant le nombre de vibration par seconde de la note.
Voici le tableau de fréquence des principales note de musique (sol 3 : cad le 3° octave en clé de sol).
Il y a un rapprochement entre le nombre d’or et l’une des gammes les plus célèbres : la gamme naturelle ou encore appelée la gamme des physiciens ou gamme de Zarlin (c’est le physicien qui en fixa les caractéristiques).
Cette gamme comporte 5 intervalles d’un ton :
- do1-ré
- ré-mi
- fa-sol
- sol-la
- la-si
Et 2 intervalles d’un demi ton :
- si-fa
- si-do2
On remarque que la proportion du sol et du la sont 2 rapports de 2 termes consécutifs de la suite de Fibonacci, respectivement 3/2 et 5/3. Pour plus de facilité, nous noterons cette suite v(n) et sa définition est telle que v(n) = u(n+1)/u(n) ou u (n+1) et u(n) sont des termes de la suite de Fibonacci.
N.B : do2 est à l’octave de do1
2) – Fibonaci est de retour
La superposition de 2 notes s’appelle un intervalle. Il y en a plusieurs types dans la gamme de Zarlin :
- l’unisson : le rapport vaut 1/1
- l’octave : le rapport vaut 2/1
- la tierce mineure : le rapport vaut 6/5
- la tierce majeure : le rapport vaut 5/4
- la quarte : le rapport vaut 4/3
- la quinte : le rapport vaut 3/2
- la sixte mineure : le rapport vaut 5/3
- la sixte majeure : le rapport vaut 8/5
Nous allons nous intéresser aux quintes et aux sixtes mineures. En effet, on obtient de 2 termes consécutifs de la série v(n) obtenue grâce à la suite de Fibonacci (1, 1, 2, 3, 5, 8, …).
Voici quelques intervalles et leur rapport :
Do-La : 5/3 => sixte mineure
Ré-Si : 5/3 => sixte mineure
Mi-Do+ : 8/5 => sixte majeure
Fa-Ré+ : 27/16
Sol-Mi+ : 5/3 => sixte mineure
La-Fa+ : 8/5 => sixte majeure
Si-Sol+ : 8/5 => sixte majeure
Do-Sol : 3/2 => quinte
Ré-La : 40/27
Mi-Si : 3/2 => quinte
Fa-Do+ : 3/2 => quinte
Sol-Ré+ : 3/2 => quinte
La-Mi+ : 3/2 => quinte
Si-Fa+ : 64/45 => quinte
3) – Création de nouvelles gammes
La série v(n) de Fibonacci ne fournit pas une gamme de Zarlin complète. En effet, il manque les intervalles de seconde majeure et de septième mineure. La solution consiste à diéser ou bémoliser les notes de la gamme de Zarlin pour obtenir une gamme chromatique (suite de 12 demi-tons contenus dans 1 octave).
On obtient alors une gamme dodécaphonique mais celle ci présente un grave inconvénient :
Ø Les demi-tons qu’elle comporte n’ont pas une valeur unique mais se répartissent 2 valeurs distinctes rendant toute transposition (opération courante en musique consistant à faire passer un texte musical d’une tonalité à une autre) impossible.
On surmonte ce problème en utilisant une gamme tempérée (gamme comportant 12 demi-tons tous rigoureusement égaux). Néanmoins, on devra renoncer à certaines qualités de la gamme de Zarlin.
Ø Par le calcul, on trouve que la mesure de l’intervalle d’un demi-on est de .
Jusqu’à une certaine époque, la gamme de Zarlin et la gamme tempérée étaient utilisées par la majorité des compositeurs. Mais une nouvelle gamme fut créée : la gamme tempérée décaphonique.
Ø Cette gamme est directement liée au nombre d’or. Chacun des dix intervalles élémentaires contenus dans l’équivalent d’une octave a pour valeur :
On peut trouver (par pure coïncidence) que : . Ces 2 nombres sont assez proches l’un de l’autre.
4) – Rythmes musicaux
Les rapports 2/1 et 3/2 sont constamment présents dans les mesures à 2, 3 et 4 temps.
Le rapport 5/3 se rencontre dans les mesures à 5 temps.
Quant au rapport 8/5, on le retrouve superposé à d’autres rapports dans certains éléments rythmiques de ma musique occidentale traditionnelle.
5) – Structure des compositions
Une composition musicale est en fait composée par 2 parties successives juxtaposées de durées inégales. Parfois, il arrive que le rapport des 2 durées (mesurées en nombre de mesures) soit égal à j.
C’est le cas du compositeur Béla Bartok.
A suivre un patch reprenant quelques uns de ces principe.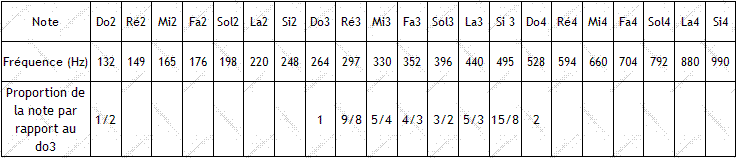
Hors ligne
#2 2006-05-13 22:00:15 Re : Suite De Fibonacci et nombre d'or en Musique
- JM Charcot
- membre
- Lieu: 1190
- Date d'inscription: 2005-12-30
- Messages: 35
- Site web
Re: Suite De Fibonacci et nombre d'or en Musique
Tiens, il y avait Elliot Sharp qui jouait sur sa basse/guitare à partir de la suite de Fibonnaci, ça dépotait bien.

http://www.panix.com/~esharp/
Hors ligne
#3 2006-05-14 10:16:00 Re : Suite De Fibonacci et nombre d'or en Musique
- tobald
- modérateur
- Date d'inscription: 2008-03-28
- Messages: 499
Re: Suite De Fibonacci et nombre d'or en Musique
Je ne connais pas cet homme mais ça m'interesse beaucoup de voir son accordage.
Bien vu !
Hors ligne
#4 2006-05-16 17:01:35 Re : Suite De Fibonacci et nombre d'or en Musique
#5 2006-08-09 13:19:22 Re : Suite De Fibonacci et nombre d'or en Musique
- tobald
- modérateur
- Date d'inscription: 2008-03-28
- Messages: 499
Re: Suite De Fibonacci et nombre d'or en Musique
Au cas ou ça interesserait quelqu'un :
Il y a un patch dans la série des ARGO qui reprend le principe des suites de Fibonacci
On y apprend que dans max :
les nombres entiers sont compris entre -2^31 et 2^31-1 (-2147483648 et 2147483647)
L'ensemble des patches ARGO de paresys sont disponibles ici :
http://perso.orange.fr/Paresys/ARGO/
(En pièce jointe le patch en question)
Hors ligne
Pages: 1
- Accueil forums
- » Max/MSP - Jitter
- » Suite De Fibonacci et nombre d'or en Musique
fil rss de cette discussion :
