- Vous n'êtes pas identifié.
Annonce
#1 2010-12-05 19:38:59 [Patch] Orgue
[Patch] Orgue
Bonsoir,
J'avais promis de contribuer aussi régulièrement que possible donc me voilà.
J'ai terminé hier mon premier synthétiseur avec Pure Data. Il simule un orgue.
Son interface est très simple : 10 sliders : les neuf premiers sont pour les harmoniques et le dernier pour le volume global. Il gère une polyphonie de 16 voix. L'outlet est la sortie sonore. Personnellement, j'aime bien y ajouter de l'écho et de la reverb. ;-)
Vous devez disposer d'un clavier MIDI pour l'utiliser.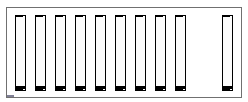
Le téléchargement se passe là : http://ompldr.org/vNm5ueA/organ.zip.
Et enfin une petit démonstration (désolé pour les clicks, mon ordi est pas super performant...).
lien vers la page de la vidéo sur youtube
Enjoy.
Dernière modification par steven (2010-12-21 14:16:40)
Hors ligne
#2 2010-12-06 10:22:57 Re : [Patch] Orgue
- Luc Sassion
- membre
- Date d'inscription: 2010-06-09
- Messages: 110
Re: [Patch] Orgue
cool
il manque quelques sur ta boiboite.
Hors ligne
#3 2010-12-16 20:48:19 Re : [Patch] Orgue
- the unguest
- nouveau membre
- Date d'inscription: 2010-12-15
- Messages: 6
- Site web
Re: [Patch] Orgue
Merci pour la polyphonie!!!! ![]()
Je galérais à trouver comment mettre ça en place, maintenant je me suis fait un petit additionneur 8 voies.
Je vais pouvoir me concentrer sur la texture dorénavant. ![]()
Hors ligne
#4 2010-12-19 18:24:04 Re : [Patch] Orgue
- akatronic
- membre
- Date d'inscription: 2008-04-03
- Messages: 39
Re: [Patch] Orgue
merci pour ce patch intéressant.
Tu pourrais remplacer les messages 1327-note et 1327-velo par $0-note et $0-velo ce qui permettra d'avoir plusieurs orgues dans le même patch.
j'ai une question : comment les harmoniques ont elles été choisies ? en particulier pourquoi 5.04 et 5.99 et 0.5 ?
Hors ligne
#5 2010-12-21 14:09:04 Re : [Patch] Orgue
Re: [Patch] Orgue
Bonjour.
J'avais déjà remplacé par $0- mais j'avais fait depuis le fichier source. C'est sûrement pour ça que ça a mis un identifiant constant. Je vais réessayer car j'ai pas trop envie de tout changer à la main ^^.
Concernant les harmoniques, je savais que je devais avoir -1 octave, quinte juste, fondamentale, octave etc... (j'ai pris les valeur de l'orgue Hammond dans Bristol). Ensuite j'ai tracé la courbe f(x) = 440 * 2 ^ ((x - 69) / 12) dans Geogebra pour avoir les fréquences en fonction des notes. Ensuite, je savais que, par exemple, pour une octave, je devais avoir 12 notes d'écarts (12 demis tons). J'ai donc pris des abscisses a et b au hasard tels que b = a + 12. Puis j'ai fait les quotient f(b) / f(a). Je me suis rendu compte que quelque soit a, f(b) / f(a) était constant. Ça me donnait donc la valeurs de l'harmonique à une octave. J'ai ensuite recommencé pour toutes les harmoniques. J'ai moi même été étonné de ne pas tomber sur des valeurs justes pour 5.04 et 5.99 mais à l'oreille, cela sonnait effectivement mieux que 5 et 6.
J'ai fait cette animation sous GeoGebra, si ça peut t'aider... http://stevenlr.tk/html/intervalle/intervalle.html
En espérant t'avoir un peu éclairé.
Edit : En fait, dans le fichier source, il fallait pas mettre $0 mais \$0. Voilà donc la nouvelle version : http://ompldr.org/vNm5ueA/organ.zip.
Dernière modification par steven (2010-12-21 14:17:33)
Hors ligne
#6 2011-01-01 15:31:02 Re : [Patch] Orgue
- akatronic
- membre
- Date d'inscription: 2008-04-03
- Messages: 39
Re: [Patch] Orgue
Merci pour ta réponse, j'ai du mal à comprendre le 69 dans ton calcul.
citation :
Ensuite j'ai tracé la courbe f(x) = 440 * 2 ^ ((x - 69) / 12)
Je pensais plutôt à une raison plus historique ou physiologique. Tous les sons intéressants pour l'oreille ne sont jamais parfaits physiquement parlant, mais je n'ai pas assez de connaissances sur les orgues.
Le $0 plante dans pas mal de versions de puredata. Ca fait parti du charme de l'appli ![]()
Hors ligne
#7 2011-01-09 19:14:27 Re : [Patch] Orgue
Re: [Patch] Orgue
Bonjour, (et désolé pour ce retard, le début d'année a été assez chargé)
Le 69 est selon la norme MIDI la note La 4. Cette note a une fréquence de 440. Et c'est pour ça que je multiplie par 440. J'aurai aussi pu mettre "x - 57" (57 étant le La 3) et multiplier par 220 ou encore 45 et 110, c'est simplement pour donner une référence connue.
Et bonne année ^^
Hors ligne
